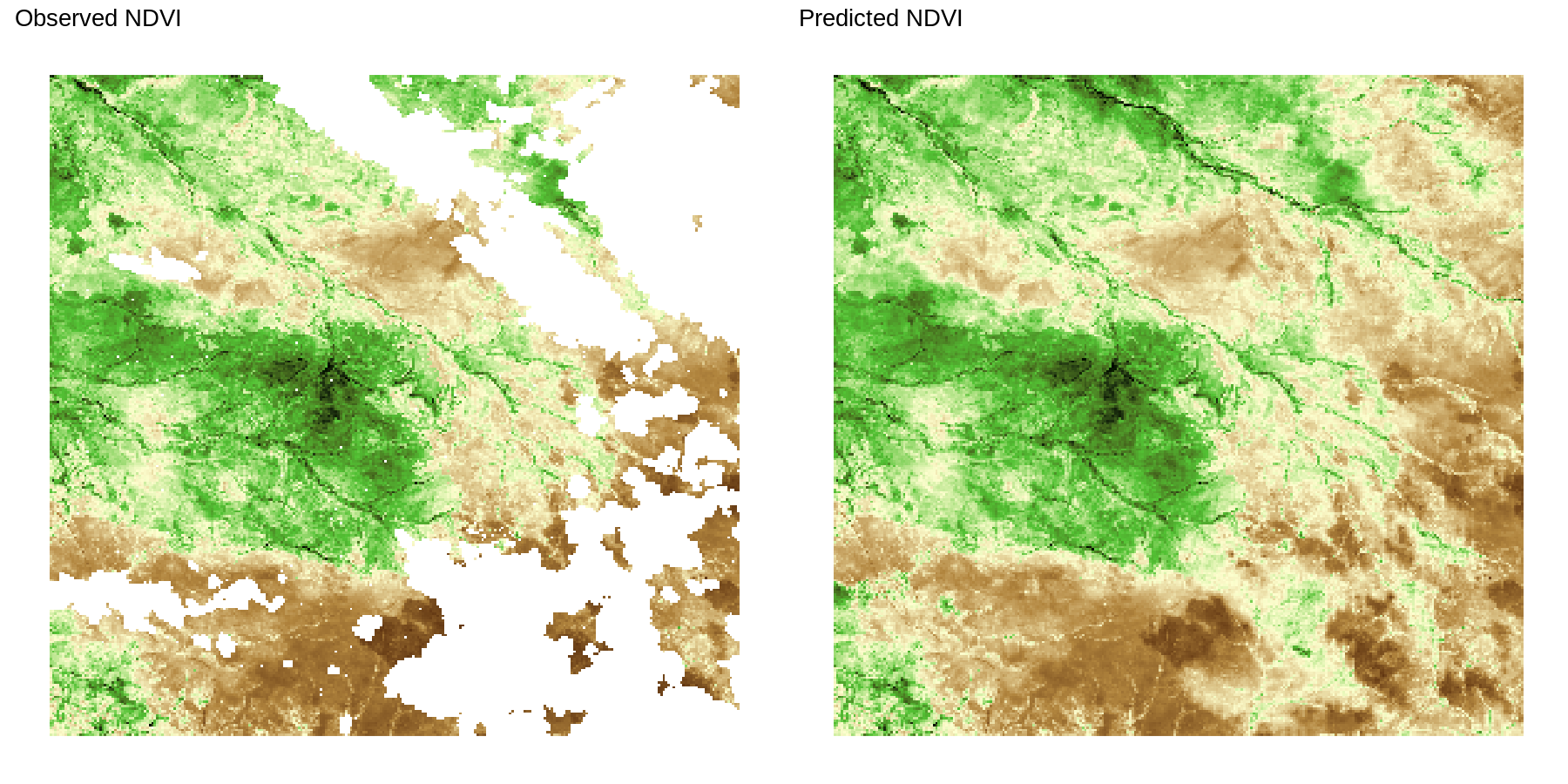
The R package for MGPs is now meshed, also available on CRAN.
meshgp is the original code/package for the JASA article. Compared to meshed, it only works on Gaussian outcomes; in the multivariate case, it uses a covariance function defined on latent domain of variables defined in Apanasovich and Genton (2010, Biometrika). In the univariate case, updates for the spatial variance are conditionally conjugate. meshed is more flexible and much more efficient. The GriPS article details the improvements.
This package will not be developed further but will remain available.
Install with devtools::install_github("mkln/meshgp").
Refer to examples in the analysis folder for some simulations and comparisons.
Notes: Tested on Ubuntu 18.04 (R-4.0.2 w/ Intel MKL 2019.5 or 2020.1) and CentOS 8.2 (R-4.0.2 w/ OpenBLAS 0.3.10). Not tested on macOS or Windows yet. On CentOS, the default OpenBLAS 0.3.3 shipping with R causes segfaults due to possible conflicts with OpenMP. With OpenBLAS 0.3.10 compiled from source (using make NO_AFFINITY=1 USE_LOCKING=1 USE_OPENMP=1) there are no issues. YMMV.
List of models that can be implemented currently:
meshgp::meshgp(): spatially-varying coefficients regression (SVC) using theZargument to store the dynamic inputs (not yet inmeshed)meshgp::mvmeshgp(): latent GP regression on multivariate outputs (better inmeshed)meshgp::meshgp_dev(): latent GP regression on univariate output with gridded reference set != observed locations (better inmeshed; also works in the multivariate case)
Citation: M. Peruzzi, S. Banerjee & A. O. Finley (2020). Highly Scalable Bayesian Geostatistical Modeling via Meshed Gaussian Processes on Partitioned Domains. Journal of the American Statistical Association, in press. DOI: 10.1080/01621459.2020.1833889
Link to arXiv version with supplement
BibTeX:
@article{doi:10.1080/01621459.2020.1833889,
author = {Michele Peruzzi and Sudipto Banerjee and Andrew O. Finley},
title = {Highly Scalable Bayesian Geostatistical Modeling via Meshed Gaussian Processes on Partitioned Domains},
journal = {Journal of the American Statistical Association},
volume = {0},
number = {0},
pages = {1-31},
year = {2020},
publisher = {Taylor & Francis},
doi = {10.1080/01621459.2020.1833889},
URL = {https://doi.org/10.1080/01621459.2020.1833889},
eprint = {https://doi.org/10.1080/01621459.2020.1833889}
}